慣性モーメント

平行軸の定理

今までは，”物体の重心を通る軸上の回転の慣性モーメント”を求めていきましたが，
　回転軸と物体の重心が一致しない場合
はどのように考えていけばいいのでしょう？

これは，平行軸の定理，と呼ばれていて，色々なサイトで説明がなされていますが，Wiki，が一番わかりやすかったです．

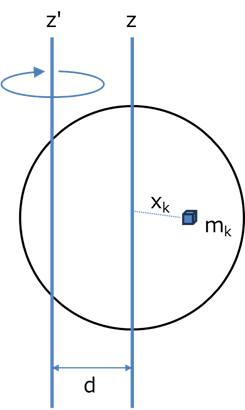
図のように，重心から，ｄ，だけズレた軸が回転軸の場合を考えます．

三次元物体の場合，慣性モーメントは，重心位置となる回転軸，z(=z'+d)，の場合，

\( \Large \displaystyle J_{center} = \int (x^2 + y^2 ) \ dM \)

となりますが，回転軸がｄだけずれたｚ‘の場合は，ｘ方向にｄだけずれている物体の座標は，x+d，となるので，

\( \Large \displaystyle J = \int \left[ (x+d)^2 + y^2 \right] \ dM \)

\( \Large \displaystyle = \int \left[ x^2+ 2dx +d^2 + y^2 \right] \ dM \)

\( \Large \displaystyle = \int ( x^2+ y^2) \ dM + 2d \int x \ dM +d^2 \int x \ dM \)

となりますが，第二項は重心の定義により，０となります．したがって，

\( \Large \displaystyle =J_{center} +Md^2 \)

となり，重心を通る場合の慣性モーメント　＋　回転軸と重心との距離の二乗の積，と簡単な計算となります．

次ページからは，平行軸の定理の検証，を検討していきます．